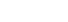差分プライバシーを用いて時系列データを秘匿化してみた
近年の生成AIや機械学習に関心が集まる中で、
IoTデバイス等によって時系列データの収集をされている方も増加傾向にあります。
一方、プライバシー保護のための法規制による制裁金が企業に課せられるケースもあり、
収集したデータの保護や秘匿化の技術に注目が集まっています。
本記事では、秘匿化に関する技術として、
時系列データに対する「差分プライバシー」を用いた秘匿化を解説いたします。
※なるべく高等数学に関しては簡略化するようにいたしますが、ノルム等の代数学を使う場面があります。予めご了承ください。
目次
はじめに
差分プライバシーとは
差分プライバシーの課題
時系列データに対する差分プライバシー
FPAkで秘匿化したデータの分析
はじめに
こんにちは。IPコミュニケーショングループのshimazaki.hです。
普段はデータ活用や分析に関しての業務に従事させていただいております。
今回は時系列データを提供いただく際に、どのように秘匿化するかについて、
実装レベルでの情報が少なかったため、私なりに情報収集したり試した内容についてお伝えいたします。
本記事は、アイソルートアドベントカレンダー2023の14日目の記事です。
差分プライバシーとは
まず、差分プライバシーについてお話します。
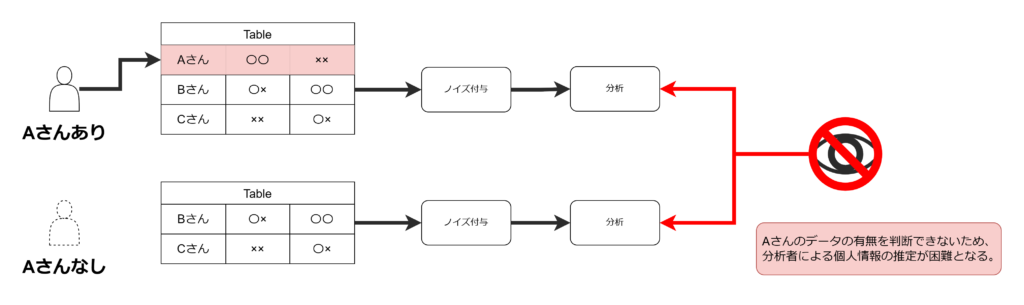
この技術は、収集したデータ(数値)に個人を特定しにくくするためノイズを付与してから分析を行うことで、
個人の特定を防ぐという仕組みです。
ここで、そもそもノイズを付与したら分析する際も正しく出ないのでは?とお考えの方は鋭い視点をお持ちです。
この仕組みでは、分析する際に統計値の有用性が失われないようなノイズを付与します。
さらに、あるデータが抜ける場合でも同じような分析結果になるようにノイズを生成します。
(差分プライバシーという名称の由来でもありますが、
あるデータが抜ける=差分から特徴を捉えられないようにプライバシー保護処理をするというのがこの技術です。)
参考資料: 差分プライバシーとは – AppleやGoogleも活用する最先端のプライバシー保護技術
もう少し詳細な内容ですが、
差分プライバシーで用いるノイズの種類は、「ラプラス分布」に従属した特性を持つノイズを用います。
(余談ですが、原著論文内ではラプラスメカニズムとして、特性の求め方込々で名称が与えられていました。)
ラプラス分布は下図のような分布で、中心が鋭利な凸となる分布で、
さらに分布の裾の幅をパラメータとして指定できる特徴を持ちます。
この特徴を用いて、あるデータが欠損した場合でも同じような分析結果となるような差分プライバシーの特性を担保しています。
引用: IkamusumeFan, 投稿者自身による著作物, CC 表示-継承 4.0, リンクによる
差分プライバシーの課題
時系列データに対して差分プライバシーを適用する場合、通常の差分プライバシーとは異なる課題が発生します。
特に、
・データ点数が多くなりがちなため、秘匿化した際のデータの質が悪化する。
・データ点の前後関係も考慮した分析を行う際に、関係性を乱すようにノイズが載るため意図した分析ができない。
この2点が主たる課題として挙げられます。
時系列データに対する差分プライバシー
そこで、FPAkと呼ばれる差分プライバシーを応用した仕組みが用いられます。
この仕組みでは、フーリエ変換を用いて時間軸から周波数軸に予め変換したデータに対してノイズを付与します。
さらに、データ点数が多くなる点に対しての解決策としては、
もともとのデータから周波数軸上で分析を行うデータ数を減らすことで対応します。
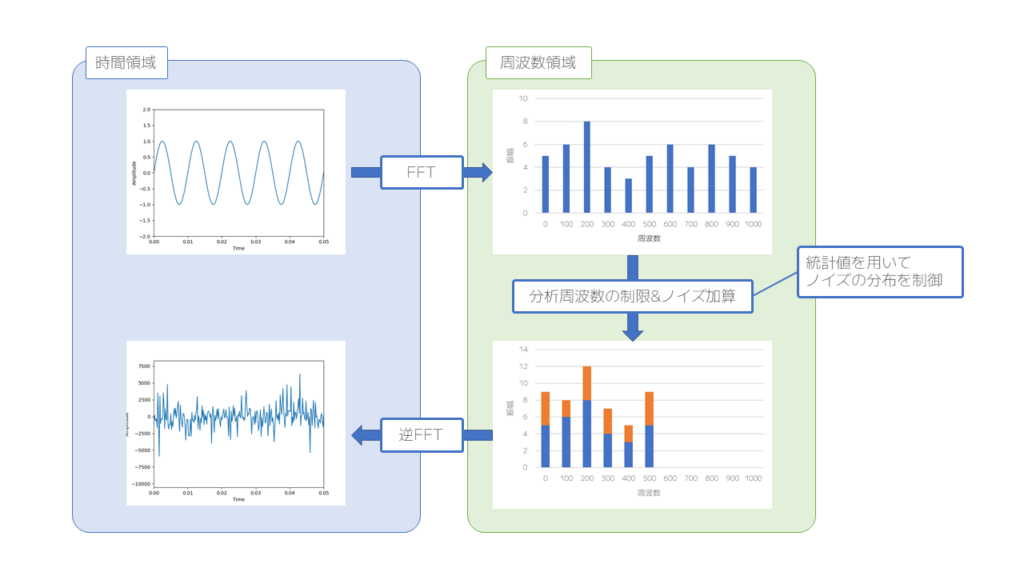
もう少し詳細を見ていきます。
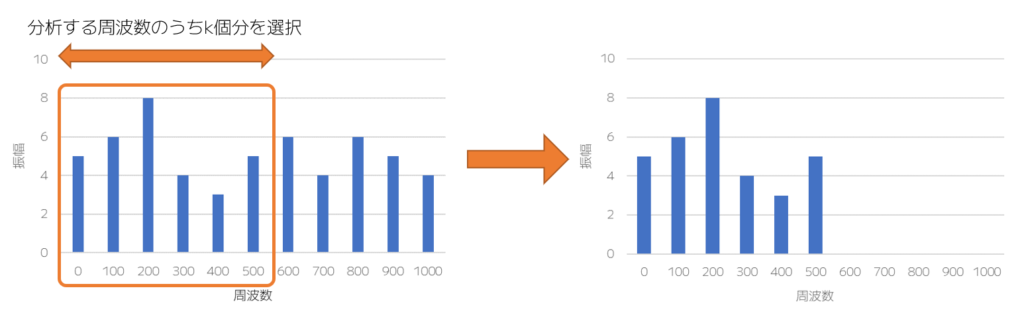
まず、データ点数の削減に関しては、下図のように周波数軸で低い周波数のものからk個分を選択します。
イメージとしては、サンプリングレートを落とすようなイメージかと考えています。
その後、データ点数を削ったデータに対し、ノイズを周波数軸上で加算していきます。
その際のラプラス分布の幅は下記の式から求めることができます。

参考資料: 差分プライバシーによる時系列データの扱い方
ここまで説明したことを、実際にPythonのコードへ落としてみると下記のような内容となります。
このコードでは、いくつかの正弦波を合成した波形に対してノイズを加算するようにしています。
次節における説明の都合上、合成波も2種類分それぞれ5つ生成しています。
import numpy as np
import pandas as pd
import scipy
"""
処理の戦略
Fsで指定したサンプリングレートで合成波を生成して、
その信号をkで指定する周波数のサンプリングレートに落としてFPAkの処理を実行する。
"""
Fs = 20000 # サンプリングレート
Nyquist_Fs = int(Fs/2) # ナイキスト周波数(グラフ表示用)
Time = 1.0 # 分析期間
F_1 = 2100 # 周波数1
F_2 = 1000 # 周波数2
F_c = 4000 # 固定しておく周波数
k = 10000 # 分析をする周波数
DATA_COUNTS = 10 # sin波の個数今回は10個生成
epsilon = 2 # ノイズの加算量を調整するパラメータ 2程度が一般的
# グラフ表示用
time_count = np.arange(0, Time, 1/Fs)
time_count_k = np.arange(0, Time, 1/k)
# 合成波の生成用関数
def sin_wave_gen(Freq_1, Freq_2, time_count):
sin_waves = []
for i in range(DATA_COUNTS):
if i < DATA_COUNTS / 2:
sin_waves.append(1.0 * np.sin(2.0 * np.pi*Freq_1*time_count) + 1.0 * np.sin(2.0 *np.pi*F_c*time_count))
else:
sin_waves.append(1.0 * np.sin(2.0 * np.pi*Freq_2*time_count) + 3.0 * np.sin(2.0 *np.pi*F_c*time_count))
sin_waves = np.array(sin_waves)
return sin_waves
# 合成波の生成
sin_wave = sin_wave_gen(Freq_1=F_1, Freq_2=F_2, time_count=time_count)
# ダウンサンプリング関数
# https://qiita.com/sumita_v09/items/808a3f8506065639cf51 を参考に作成
def downsampling(target_rate: int, data: np.array, fs: int) -> (np.array, int):
# 間引くサンプル数を決める
decimation_sampleNum = int((fs/target_rate)-1)
# FIRフィルタの用意をする
nyqF = (target_rate)/2.0 # 変換後のナイキスト周波数
cF = (target_rate/2.0-500.)/nyqF # カットオフ周波数を設定(変換前のナイキスト周波数より少し下を設定)
taps = 511 # フィルタ係数(奇数じゃないとだめ)
b = scipy.signal.firwin(taps, cF) # LPFを用意
# フィルタリング
data = scipy.signal.lfilter(b, 1, data)
# 間引き処理
down_data = []
for i in range(0, len(data), decimation_sampleNum+1):
down_data.append(data[i])
return (down_data)
# 合成波をダウンサンプリング
sin_wave_ds = np.array([downsampling(target_rate=k, data=sin_wave[i,:], fs=Fs) for i in range(DATA_COUNTS)])
# ラプラスノイズの幅を指定するパラメータを算出
q_d = np.array([sin_wave_ds[:,i] - sin_wave_ds[:,i-1] for i in range(1,len(time_count_k))])
q_L2 = np.array([np.linalg.norm(q_d[:,i], ord=2) for i in range(DATA_COUNTS)])
lamda = np.array(np.sqrt(k/4*Time) * q_L2 / epsilon)
# ランダム生成器の宣言
rng = np.random.default_rng()
# ラプラスノイズ生成関数
def laplace_noise_gen(k, lamda) -> np.ndarray:
random_array = np.zeros([DATA_COUNTS, k])
for i in range(DATA_COUNTS):
random_array[i,:k] = rng.laplace(0, lamda[i], k)
return random_array
# ラプラスノイズを生成
random_array = laplace_noise_gen(k=k, lamda=lamda)
# 各波形をフーリエ変換
ffted_wave = (2/len(time_count_k)) * np.fft.fft(sin_wave_ds)
ffted_rdmarray = (2/len(time_count_k)) * np.fft.fft(random_array)
# plot用の周波数軸も生成
freq_range = np.fft.fftfreq(n=k, d=1/k)
# ラプラスノイズを加算
ffted_privacy_wave = ffted_wave + ffted_rdmarray
# 時間波形へ逆変換
privacy_wave = np.fft.ifft(ffted_privacy_wave) / (2/len(time_count_k))
privacy_wave = privacy_wave.real
FPAkで秘匿化したデータの分析
ここまでの内容を踏まえて、実際にデータ分析を行った際にどのような結果となるかを見てみましょう。
先ほどのコードを本に2種類の合成波を作成し、各振幅レベルの平均を用いて次元を減らしてから、
k-means法により分類できるか試してみます。
生成する正弦波としては前節のコードにて生成したの2種類です。
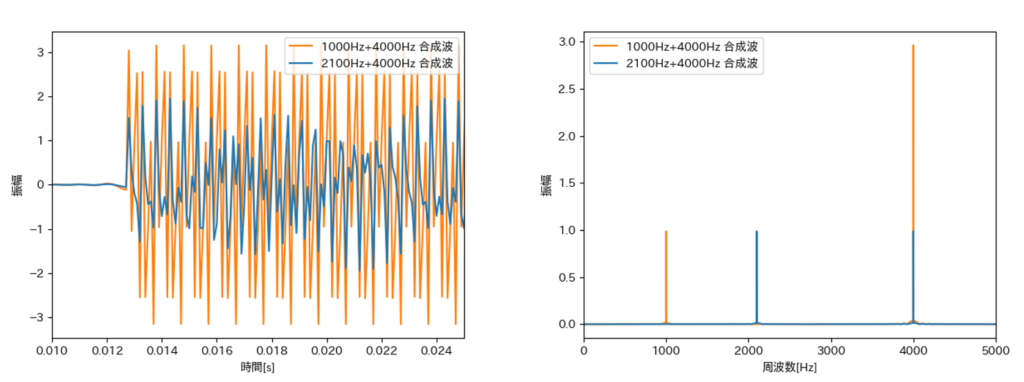
前節で秘匿化した合成波の各周波数における平均振幅を算出し、
それら平均振幅値を元にクラスタリングするコードを下記に記載します。
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# 絶対値を取って分析ができる状態に持ってく
fft_len = int(len(ffted_privacy_wave[0,:])/2) - 1
# 振幅の平均値を算出(1次元に平均値を格納、2次元は0埋めしておく)
ffted_privacy_wave_abs = np.abs(ffted_privacy_wave[:,:fft_len])
ffted_privacy_wave_mean = np.zeros((2,DATA_COUNTS))
ffted_privacy_wave_mean[0,:] = np.array([np.mean(ffted_privacy_wave_abs[i,:]) for i in range(DATA_COUNTS)])
# k-means法でクラスタリング
cls_privacy = KMeans(n_clusters=2).fit_predict(ffted_privacy_wave_mean.T)
# グラフ表示用に成形
cls_privacy_pca1 = ffted_privacy_wave_mean[0:2,:].T #
df_privacy_pca = pd.DataFrame(cls_privacy_pca1, columns=["amplitude_mean","zero"])
df_privacy_class = pd.DataFrame(cls_privacy, columns=["class"])
df_privacy = pd.concat([df_privacy_pca, df_privacy_class], axis=1)
# グラフ表示
fig, ax = plt.subplots()
for name_p, group_p in df_privacy.groupby('class'):
ax.plot(group_p.amplitude_mean, group_p.zero, marker='o', linestyle='', ms=8, label=name_p)
ax.legend()
plt.xlabel('振幅平均')
plt.ylabel('-')
plt.show()
実際の結果としては、下図のような形となります。
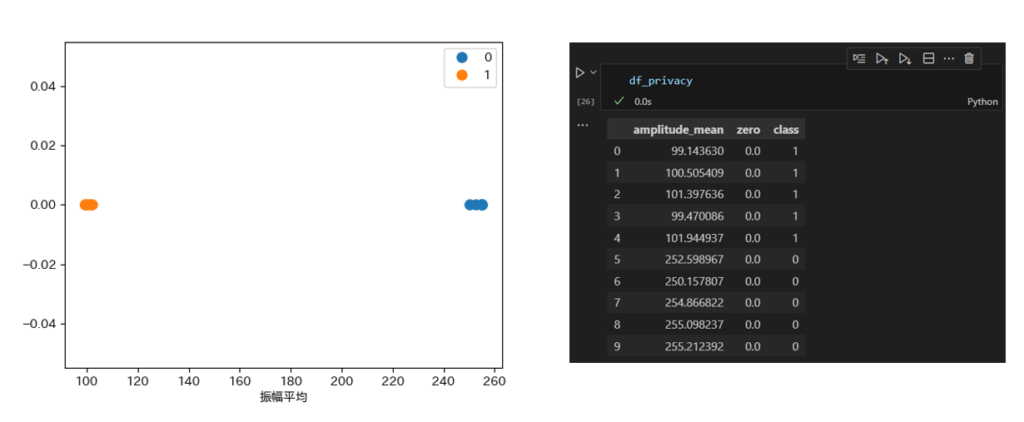
図のように今回の例ですと、振幅に大きく差が見受けられるため、
想定通りの2種類のクラスタに分類をすることができました。
このような形でデータを秘匿化することで、
分析者に対して1つ1つのデータの特徴量を特定されにくい形で分析を行うことができます。
本記事をご覧いただいた皆さんもセキュアにデータを収集して、
業務改善やデータ分析に役立てていただければと思います。
長くなりましたが、最後までご覧いただきありがとうございました。